Introduction à Numpy

Qu’est-ce que Numpy?

Numpy (Numerical Python) est une bibliothèque pour le langage Python, ajoutant le support de grands tableaux (listes) ainsi qu’une large collection de fonctions mathématiques de haut niveau pour les opérer.
C’est une bibliothèque essentielle pour la science des données.

Numpy est un module Python qui s’importe comme tous les autres. De ce fait, il suffit d’écrire et d’éxecuter le code ci-dessous dans une cellule sur Jupyter Notebook afin d’importer cette librairie.

import numpy as np

L’un des avantages de Numpy est qu’il travaille directement avec les tableaux (ou listes) et gère lui-même les boucles nécessaires aux calculs. Cela rend le code plus léger et permet une exécution plus rapide.

Les listes Numpy - tableau ndarray

Avec Numpy, il existe un équivalent plus puissant des listes python, les ndarray. Comme les listes, il est possible d’accéder aux valeurs du tableau avec des [], il est également possible de faire des tableaux à plusieurs dimensions.

Ces tableaux sont généralement construits à partir de liste python.

nd_array = np.array([10,20,30,40,50,60])

print(f"{nd_array[3]}")
print(f"{nd_array[3:5]}, {type(nd_array[3:5])}")

40
[40 50], <class 'numpy.ndarray'>

Conversion des listes en tableau ndarray

Il est possible de convertir une liste python en ndarray et inversement:

liste = [10,20,30,40,50,60]
nd_array = np.array(liste)
conversion_liste = nd_array.tolist()

print(type(liste))
print(type(nd_array))
print(type(conversion_liste))

<class 'list'>
<class 'numpy.ndarray'>
<class 'list'>

Fonctions statistiques pour les tableaux

Voici quelques fonctions statistiques de Numpy:

print(f"Moyenne: {np.mean(liste)}")
print(f"Somme: {np.sum(liste)}")
print(f"Produit: {np.prod(nd_array)}")
print(f"Valeur minimum: {np.min(liste)}")
print(f"Valeur maximum: {np.max(nd_array)}")

Moyenne: 35.0
Somme: 210
Produit: 720000000
Valeur minimum: 10
Valeur maximum: 60

Remarquez que ces fonctions peuvent prendre en argument des ndarray Numpy ou des list python.

Les opérateurs avec tableau

Contrairement aux listes, les opérations entre un tableau et une valeur numérique sont possibles.

Dans ce cas, l’opération est faite élément par élément du tableau.

# ajoute 10 a tous les elements du tableau
nd_array_2 = nd_array + 10
print(nd_array_2)

# multiplie par 10 tous les éléments du tableau
nd_array_3 = nd_array * 10
print(nd_array_3)

# aditionne 2 tableaux élément par élément
nd_array_4 = nd_array + nd_array
print(nd_array_4)

[20 30 40 50 60 70]
[100 200 300 400 500 600]
[ 20  40  60  80 100 120]

Attention

Si vous faites ces opérations avec une liste python, vous obtiendrez une erreur, votre code ne s’exécutera pas.

liste_2 = liste + 10

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
/tmp/ipykernel_246843/682676413.py in <module>
----> 1 liste_2 = liste + 10

TypeError: can only concatenate list (not "int") to list

Génération de tableau numpy

Il existe de nombreux cas où l’on peut avoir besoin de tableaux remplis de valeurs respectant des propriétés spécifiques.

Avec les boucles, nous avons vu l’intérêt de générer un tableau de valeurs pour accéder à une liste par ses indices, en utilisant la fonction range().

Les fonctions suivantes nous seront utiles pour tracer des graphiques avec Matplotlib.

np.arange()

C’est l’équivalent de la fonction python de base range(). Ses arguments sont les mêmes: minimum, maximum et pas. Mais elle retourne un ndarray.

x = np.arange(-10, 10, 0.5)
print(type(x))
print(x)

<class 'numpy.ndarray'>
[-10.   -9.5  -9.   -8.5  -8.   -7.5  -7.   -6.5  -6.   -5.5  -5.   -4.5
  -4.   -3.5  -3.   -2.5  -2.   -1.5  -1.   -0.5   0.    0.5   1.    1.5
   2.    2.5   3.    3.5   4.    4.5   5.    5.5   6.    6.5   7.    7.5
   8.    8.5   9.    9.5]

np.linspace()

La fonction linspace() génère un tableau de valeurs entre deux bornes, avec un nombre d’éléments spécifié en paramètre, ce qui permet de calculer automatiquement le pas entre chaque valeur.

À l’inverse, la fonction arange() prend un pas en paramètre, mais c’est la taille du tableau qui est déterminée en fonction de ce pas.

x = np.linspace(-10, 10, 50)
print(type(x))
print(x)

<class 'numpy.ndarray'>
[-10.          -9.59183673  -9.18367347  -8.7755102   -8.36734694
  -7.95918367  -7.55102041  -7.14285714  -6.73469388  -6.32653061
  -5.91836735  -5.51020408  -5.10204082  -4.69387755  -4.28571429
  -3.87755102  -3.46938776  -3.06122449  -2.65306122  -2.24489796
  -1.83673469  -1.42857143  -1.02040816  -0.6122449   -0.20408163
   0.20408163   0.6122449    1.02040816   1.42857143   1.83673469
   2.24489796   2.65306122   3.06122449   3.46938776   3.87755102
   4.28571429   4.69387755   5.10204082   5.51020408   5.91836735
   6.32653061   6.73469388   7.14285714   7.55102041   7.95918367
   8.36734694   8.7755102    9.18367347   9.59183673  10.        ]

Tracer des fonctions

Numpy et Matplotlib sont deux librairies qui fonctionnent bien ensemble, les fonctions de Matplotlib savent utiliser les ndarray aussi bien que les listes python.

Les fonctions mathématiques

Voici un ensemble de fonctions mathématiques disponibles dans Numpy:

Fonction	Inverse
`np.sin()`	`np.asin()`	fonction sinus et son inverse par éléments
`np.cos()`	`np.acos()`	fonction cosinus et son inverse par éléments
`np.tan()`	`np.atan()`	fonction tangeante et son inverse par éléments
`np.exp()`	`np.log()`	fonction exponentielle et logarithmique par éléments

Pour une version plus exhaustive, voir la documentation officielle

On peut utiliser ces fonctions comme vous le feriez sur votre calculatrice, c’est à dire en donnant une valeur, on obtient en retour le résultat de cette fonction.

$$ y = sin(0) $$ $$ y = cos(0) $$ $$ y = sin(\pi) $$ $$ y = cos(\pi) $$

print(round(np.sin(0),2))
print(round(np.cos(0),2))
print(round(np.sin(np.pi),2))
print(round(np.cos(np.pi),2))

0.0
1.0
0.0
-1.0

On peut également fournir un tableau de valeur, alors la fonction va calculer le résultat de chacun des éléments du tableau.

x = np.linspace(-10, 10, 50)
y_sin = np.sin(x)
print(y_sin)

[ 0.54402111  0.16628279 -0.23877532 -0.60460332 -0.8710967  -0.99447137
 -0.9544572  -0.75762842 -0.43632343 -0.04333173  0.35677924  0.6982724
  0.92504137  0.99982867  0.91034694  0.67129779  0.32195632 -0.08028167
 -0.46932961 -0.78126802 -0.96484631 -0.98990308 -0.85232157 -0.57470604
 -0.20266794  0.20266794  0.57470604  0.85232157  0.98990308  0.96484631
  0.78126802  0.46932961  0.08028167 -0.32195632 -0.67129779 -0.91034694
 -0.99982867 -0.92504137 -0.6982724  -0.35677924  0.04333173  0.43632343
  0.75762842  0.9544572   0.99447137  0.8710967   0.60460332  0.23877532
 -0.16628279 -0.54402111]

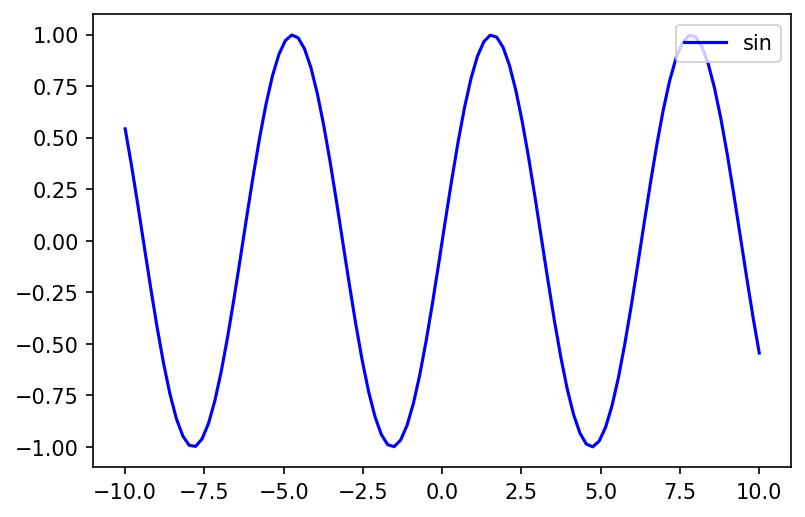
Avec ces valeurs, on a tout ce qu’il faut pour tracer la fonction :

$$ y = sin(x) $$

x = np.linspace(-10, 10, 100)
y_sin = np.sin(x)

plt.plot(x,y_sin, color="b", label="sin")

plt.legend(loc="upper right")
plt.show()

Les polynômes

Numpy offre une fonction pour utiliser des polynômes de degrée n, la fonction np.poly1d(). Elle prend en paramètre un tableau qui contient les coéfficients du polynome par ordre décroissant de puissance.

Pour générer le polynôme suivant dans numpy:

$$ y = x^2 + x -2 $$

Il faut utiliser la liste des coéfficients [1, 1, -2], on obtient alors le code suivant:

polynome = np.poly1d([1, 1, -2])
print(polynome)
print(f"Les racines de ce polynôme sont: {polyome.r}")
print(f"La valeur de ce polynôme quand x=10 est: {polynome(10)}")

   2
1 x + 1 x - 2
Les racines de ce polynôme sont: [-2.  1.]
La valeur de ce polynôme quand x=10 est: 108

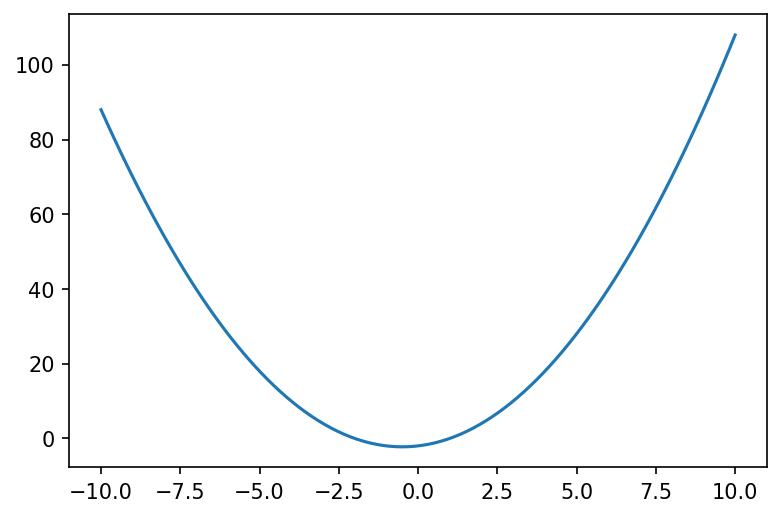
Une fois le polynôme défini, on peut l’utiliser de la même manière que les fonctions mathématiques vues ci-dessus.

x = np.linspace(-10, 10, 100)
y = polynome(x)

plt.plot(x, y)
plt.savefig('polynome.jpg', dpi=150, bbox_inches="tight")
plt.show()

Atelier

Atelier Numpy